Der logistische CASUS
Hintergrund und Fragestellung:
Der „Cardiac Surgery Score“ (CASUS) (Tabelle 1) wurde von uns erstmals im Jahr 2005 als additives Modell publiziert [6] und anhand von 6007 Patienten validiert [5]. Unter seiner einfachen additiven Berechnung leidet die Genauigkeit. Wir entwickelten daher ein logistisches Modell, das auf ausführlichen statistischen Methoden basiert und eine prozentgenaue Überlebenswahrscheinlichkeit eines individuellen Patienten erzielt. Die einfache, computergestützte Berechnung ist weiterhin gewährleistet. Wir analysierten ob der logistische CASUS seinem additiven Vorgängermodell hinsichtlich der statistischen Genauigkeit überlegen ist und prüften beide Modelle in der täglichen Praxis.
Studiendesign und Untersuchungsmethoden:
Diese prospektive Studie erfasst alle Patienten (≥ 18 Jahre), die zwischen dem 1. Januar 2007 und dem 31. Dezember 2009 nach einer Herzoperation auf unserer Intensivstation behandelt wurden. Die Ethikkomission der Friedrich-Schiller-Universität Jena stimmte dem Studienantrag zu (Nr.: 2809-05/10). Wir betrachteten ausschließlich den ersten Aufenthalt jedes Patienten. Alle Daten wurden dem Qualitätskontrollsystem QIMS 2.0b (Universitätskrankenhaus Münster, Deutschland) und dem Intensivstationssystem COPRA 5.2 (COPRASYSTEM GmbH, Sasbachwalden, Deutschland) entnommen und einer ausführlichen Kontrolle unterzogen. Als Studienendpunkt wurde die Intensivletalität bestimmt. Die Berechnung beider Modelle basiert, analog zum APACHE II System [9], auf dem pathophysiologischsten Wert eines jeden Tages.
Der logistische CASUS ermittelt durch Berechnung einer logistischen Gleichung einen individuellen Prozentsatz der Sterblichkeitswahrscheinlichkeit. Die vorhergesagte Sterblichkeit ist ℮(β0+∑βi*Xi)/(1+℮(β0+∑βi*Xi)), wobei β0 die Konstante der logistischen Gleichung und βi den spezifischen Koeffizienten jeder einzelnen Variable Xi darstellt (Tabelle 2). Xi der sechs kontinuierlichen Variablen (PaO2/FiO2-Ratio, Serumkreatinin, Serumbilirubin, PAR (HF x ZVD/MAD), Serumlaktat und Thrombozytenzahl) korrespondiert mit den Patientendaten. Während Xi=1 für die fünf kategorialen Variablen (CVVH/Dialyse, IABP, Ventrikuläres Assist Device, neurologischer Status, Intensivtag), die mit einem spezifischen βi Wert (Tabelle 2) verbunden sind.
Die statistische Analyse wurde mit SPSS Version 18 (SPSS Inc, Chicago, IL, USA) durchgeführt. Alle Grafiken wurden mit Hilfe von SigmaPlot 11.0 (Systat Software, San Jose, CA 95110 USA) erstellt. Es wurde eine Datenanalyse auf unabhängige Stichproben mit dem zweiseitigen „Student’s t-test“ durchgefühert. Der Kolmogorov-Smirnov Test zeigte eine Normverteilung der kontinuierlichen Daten. Ein p-Wert von < 0.05 wurde als signifikant definiert. Die Diskriminierung wurde mit Receiver Operating Characteristic (ROC) Kurven, die die Sensitivität („richtig Positive“) gegen die 1-Spezifität („falsch Positive“) abbilden, untersucht. Die Fläche unter der ROC Kurve (Area Under the receiver operating characteristic Curve (AUC)) reflektiert die Fähigkeit eines Modells zwischen „Überlebenden“ und „Verstorbenen“ zu unterscheiden. Während Werte > 0.8 auf eine gute diskriminative Fähigkeit hindeuten, entsprechen Werte von 0.5 (diagonale Linie) dem Zufall. Ein Vergleich der ROC Kurven wurde mit der Methode nach DeLong et al. [3] durchgeführt. Die Werte des Geamtprozentsatzes der „Richtigen“ in der Klassifizierungstabelle (Overall Correct classification (OCC)) wurden ebenfalls errechnet. Wir untersuchten die Kalibrierung anhand des Modells von Grunkemeier [8], als Verhältnis von tatsächlicher (observed (O)) zu vorhergesagter (expected (E)) Letalität.
Ergebnisse:
Die vorliegende Studie erfasst 4054 Patienten, darunter 29.0 % (n = 1175) Frauen. Die Intensivletalität lag bei 5.8 % (n = 235), das mittlere Alter bei 67.2 ± 10.9 Jahre (19 – 89 Jahre). Tabelle 3 erfasst die Art der operativen Eingriffe. Die mittlere Liegedauer betrug 4.6 ± 7.0 Tage (1 - 189 Tage, Median 2.0 Tage, 75th Percentile 4.0 Tage). Der präoperativ erhobene mittlere, logistische EuroSCORE lag bei 9.9 ± 12.9 (Median 5.3, 75th Percentile 11.4).
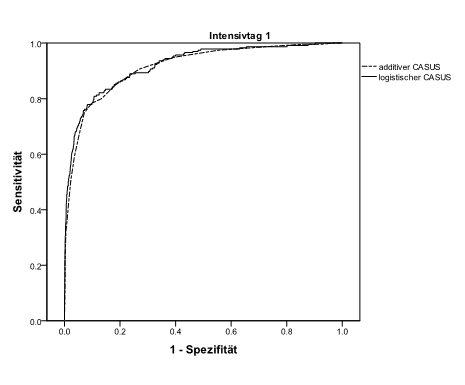
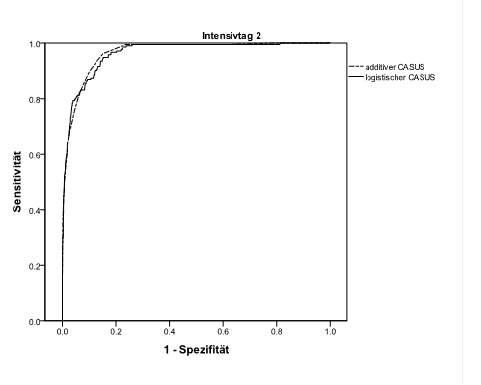
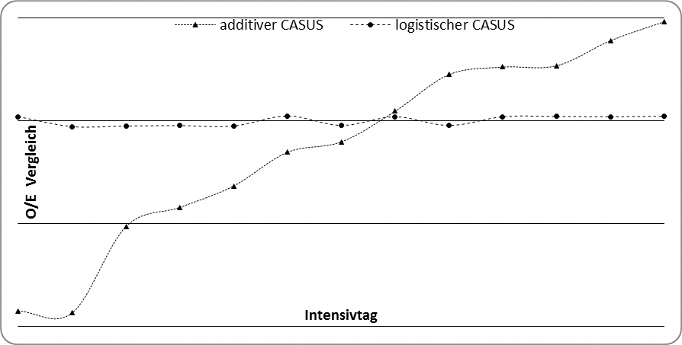
Wir ermittelten an allen Tagen eine gute Diskriminierung beider Systeme (logistisch: ≥ 0.874; additiv: ≥ 0.865). Die besten Ergebnisse wurden am zweiten Tag ermittelt (additiv: 0.966; logistisch: 0.963). Der Vergleich beider Modelle mit der DeLong Methode zeigte einen signifikanten Unterschied der ROC-Werte zu Gunsten des logistischen Modells an den Tagen 5 bis 7 und 11 bis 13 (Tabelle 4; Grafik 1). Die besten Ergebnisse bei der OCC wurden am zweiten Tag festgestellt (logistisch: 96.8 %; additiv: 96.6 %). Das logistische Modell zeigt an allen Tagen eine exzellente Kalibrierung (Tabelle 4, Grafik 2). Das additive Modell überschätzt die Sterblichkeit während der ersten Woche des Aufenthalts und unterschätzt das Risiko von Tag 9 bis Tag 13. Es gibt keinerlei fehlende Daten. In Tabelle 4 sind die OCC, die diskriminative Fähigkeit, der Vergleich der AUCs und die Kalibrierung beider CASUS Modelle zusammengefasst.
Diskussion:
Der Einsatz der Herz-Lungen-Maschine kann bei kardiochirurgischen Patienten zu pathophysiologischen Entgleisungen wie zum Beispiel eine überschiessende systemische Entzündungsreaktion („SIRS“) führen [17, 18]. Dies kann Einfluss auf den weiteren klinischen Verlauf haben [19]. Zur weiteren Stabilisierung kann eine verlängerte Beatmungsdauer [10, 15] mit erforderlicher Analgosedierung, die die Erhebung der Glasgow Coma Scale einschränkt [12], erforderlich sein. Um diese speziellen Umstände zu erfassen wurde der additive CASUS [6] entwickelt. Das Ziel der vorliegenden Studie war die Verbesserung seiner Genauigkeit, durch die Weiterentwicklung zu einem logistischen Scoresystem. Obwohl unsere Studie über 18445 Einzelfalleinträge verfügt, analysierten wir nur die ersten 13 Intensivtage, um statistische Genauigkeit zu gewährleisten.
Warum brauchen wir ein logistisches Risikomodell?
Die Vorteile des logistischen CASUS können mittels eines Beispiels und anhand von klinischen Daten veranschaulicht werden. Zwei Patienten haben nach einer einfachen Klappenoperation einen additiven CASUS von elf Punkten (Tabelle 5). Jedoch hat Patient A eine Sterblichkeitswahrscheinlichkeit von 14.9 % und Patient B von 75.9 %. Natürlich ist jeder Intensivverlauf unterschiedlich, doch ist es offensichtlich, dass der additive CASUS die Länge des Aufenthalts auf der Intensivstation nicht wiedergeben kann.
Durch einfaches Zusammenzählen der individuellen, additiven CASUS Werte (Tabelle 1), erhält man eine Gesamtsumme zwischen 0 und 40 Punkten, die per se nichts über die absolute Sterblichkeitswahrscheinlichkeit aussagt.
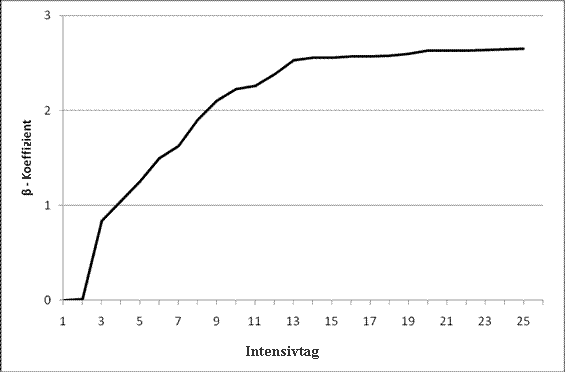
Wir berechneten exemplarisch den logistischen CASUS für Patient B. Schritt (1) zeigt die logistische Gleichung: ℮ (β0 + ∑βi * Xi) / (1 + ℮ (β0 + ∑βi * Xi)). Wir demonstrieren eine Variation der Gleichung in Schritt (2) durch Integrieren der βi-Koeffizienten: ℮ (β0 + ∑(βIntensivtag * Xi) + (βCVVH * Xi) + (βKreatinin * Xi) + (βBilirubin * Xi) + (βOxygenierungsindex * Xi) + (βNeurologischer Status * Xi) + (βThrombozyten * Xi) + (βLaktat * Xi) + (βPAR * Xi) + (βIABP * Xi) + (βVAD * Xi)) / (1 + ℮ (β0 + ∑(βIntensivtag * Xi) + (βCVVH * Xi) + (βKreatinin * Xi) + (βBilirubin * Xi) + (βOxygenierungsindex * Xi) + (βNeurologischer Status * Xi) + (βThrombozyten * Xi) + (βLaktat * Xi) + (βPAR * Xi) + (βIABP * Xi) + (βVAD * Xi))). In Schritt (3) setzten wir β0 und die Werte der elf Xi Variablen mit ihren spezifischen βi-Koeffizienten ein: ℮ (-5.6412079 + ∑ (2.5289064*1) + (0.4109223*1) + (0.3063634*1.58) + (0.2214784*12.75) + (-0.0013498*451) + (0*1) + (-0.0042251*251) + (0.2115760*1.5)+ (0.0642751*29.3823) + (0*1) + (0*1)) / (1 + ℮ (-5.6412079 + ∑ (2.5289064*1) + (0.4109223*1) + (0.3063634*1.58) + (0.2214784*12.75) + (-0.0013498*451) + (0*1) + (-0.0042251*251) + (0.2115760*1.5)+ (0.0642751*29.3823) + (0*1) + (0*1))). Der Prozentsatz der Sterblichkeitswahrscheinlichkeit für Patient B beträgt 75.9 %. Wir integrierten die neue Variable „Intensivtag” in das logistische Modell, um den negativen Effekt eines verlängerten Intensivaufenthalts zu erfassen. Der β-Koeffizient dieser Variable zeigt einen ansteigenden Verlauf bis zum 13. Intensivtag. Danach konnten wir keinen signifikanten Anstieg feststellen (Grafik 3).
Die beiden Modelle in der täglichen Praxis
Die größte Schwäche des additiven Modells liegt in der Vernachlässigung der Dauer des Intensivaufenthalts. Viele Funktionsstörungen der Organe manifestieren sich erst zu einem späteren Zeitpunkt des Intensivverlaufs. Dies gilt vor allem für Patienten, bei denen ein elektiver Eingriff vorgenommen wurde, da diese Patienten im Normalfall bei Aufnahme auf die Intensivstation keine globalen Funktionsstörungen haben [11]. Die Ausprägung einer Funktionsstörung und die Anzahl der davon betroffenen Organe korrelliert stark mit einer steigenden Sterblichkeitswahrscheinlichkeit [13, 7, 16]. Der „logistische Cardiac Surgery Score“ bewertet Funktionsstörungen, durch das Gewichten der einzelnen Variablen des additiven Modells, individuell. In Kombination mit der Erfassung eines verlängerten Intensivaufenthalts kann eine realistische Sterblichkeitswahrscheinlichkeit ermittelt werden. Auf dem logistischen Modell basierende Verlegungsstrategien, könnten verhindern, dass gefährdete Patienten auf die Normalstation verlegt werden. Das garantiert nicht nur eine geringere Anzahl an Rückverlegungen auf die Intensivstation sondern auch eine Eindämmung verlängerter Krankenhausaufenthalte. Beide Komplikationen sind eng mit einer erhöhten Sterblichkeit verbunden [2, 14].
Die Gründe der statistischen Unterschiede
Grunkemeier führte die qualitative Kalibrierung anhand des O/E-Verhältnises ein [1]. In unserer Studie konnten wir mit dieser Methode deutliche Unterschiede bei dem additiven Modell nachvollziehen, bei dem wir eine Überschätzung der Sterblichkeit an den ersten fünf Intensivtagen und eine Unterschätzung an den Tagen neun bis 13 feststellten (Grafik 2). Beide Scores erreichten eine gute diskriminative Fähigkeit, allerdings war das logistische Modell ab dem vierten Intensivtag dem additiven überlegen. Die statistische Überlegenheit des logistischen CASUS in Kalibrierung und Diskriminierung ist nicht überraschend. Die relevanten Organsysteme der Modelle haben einen unterschiedlichen Einfluss auf den Intensivverlauf. Diese Flexibilität kann von dem additiven Modell nicht adäquat gewährleistet werden. So haben zum Beispiel die Variablen „Herzunterstützungssysteme“ und „intraaortale Ballonpumpe“ in dem additiven Modell beide vier Punkte. Das logistische Modell hingegen verleiht den beiden Variablen duch seine β-Koeffizienten (Herzunterstützungssysteme: 2.2976240; intraaortale Ballonpumpe: 0.6770239) sehr unterschiedliche Gewichtungen. Des Weiteren kann das logistische Modell einen verlängerten Intensivverlauf durch die neue Variable „Intensivtag“ besser wiederspiegeln als das additive.
Wo liegen die Grenzen eines Risikomodells?
Wir weisen darauf hin, dass Therapien nicht aufgrund von hohen Werten in Risikomodellen eingestellt werden dürfen, da sie auf statistischen Methoden basieren und Entscheidungen auf der Intensivstation individuell getroffen werden müssen [4].
Schlussfolgerung für die praktische Anwendung:
• Beide CASUS Varianten sind verlässliche Risikomodelle für alle Arten herzchirurgischer Patienten.
• Das logistische Modell zeigt nennenswerte statistische Überlegenheit und bietet mit seiner individuellen Gewichtung der Organsysteme eine präzise und realistische Risikoeinschätzung in Prozent.
• Beide CASUS Varianten könnten als Expertensystem zum Qualitätsvergleich von Intensivstationen dienen.
• Eine verbesserte Kommunikation mit Patienten und Angehörigen könnte dadurch ermöglicht werden.
• Das additive Modell kann ohne hochspezialisierte Informationstechnologie und komplexe Mathematik berechnet werden und bleibt daher „Goldstandard” in Bereichen, in denen die nötige Informationstechnologie nicht vorhanden ist.
• Unter der Verwendung eines „persönlichen digitalen Assistenten“ kann auch der logistische CASUS problemlos am Patientenbett berechnet werden.
• Eine externe Validierung des logistischen CASUS in einer großen Multicentre Studie ist wünschenswert.
Literatur:
1. Anderson RP, Jin R, Grunkemeier GL (2003) Understanding logistic regression analysis in clinical reports: an introduction. Ann Thorac Surg 75:753-757
2. Chung DA, Sharples LD, Nashef SAM (2002) A case-control analysis of readmissions to the cardiac surgical intensive care unit. Eur J Cardiothorac Surg 22:282-286
3. DeLong ER, DeLong DM, Clarke-Pearson DL (1988) Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44:837-845
4. Heijmans JH, Maessen JG, Roekaerts PMHJ (2003) Risk stratification for adverse outcome in cardiac surgery. European Journal of Anaesthesiology 20:515-527
5. Hekmat K, Doerr F, Kroener A, et al (2010) Prediction of mortality in intensive care unit cardiac surgical patients. Eur J Cardiothorac Surg 38:104-109
6. Hekmat K, Kroener A, Stuetzer H, et al (2005) Daily assessment of organ dysfunction and survival in intensive care unit cardiac surgical patients. Ann Thorac Surg 79:1555-1562
7. Herbert RC, Drummond AJ, Singer J, Bernard GR, Russel JA (1993) A simple multiple organ system failure scoring system predicts mortality of patients who have sepsis syndrome. Chest 104:230-235
8. Jin R, Grunkemeier GL (2006) Does the logistic EuroSCORE offer an advantage over the additive model? Interactive CardioVascular and Thoracic Surgery 5:15-17
9. Knaus W, Draper E, Wagner D, Zimmerman J (1985) APACHE II: a severity of disease classification system. Crit Care Med 13:818-829
10. Kollef HM, Wragge T, Pasque C (1995) Determinants of mortality and multiorgan dysfunction in cardiac surgery patients requiring prolonged mechanical ventilation. Chest 107:1395-1401
11. Le Gall JR, Klar J, Lemeshow S, et al (1996) The Logistic Organ Dysfunction System: A New Way to Assess Organ Dysfunction in the Intensive Care Unit. Journal of the American Medical Association 276:802-810
12. Marik PE, Varon J (1999) Severity scoring and outcome assessment. Computerized predictive models and scoring systems. Crit Care Clin 15:633-646
13. Marshall JC, Cook DJ, Christou NV, Bernard GR, Sprung CL, Sibbald WJ (1995) Multiple Organ Dysfunction Score: a reliable descriptor of a complex clinical outcome. Crit Care Med 23:1638-1652
14. Michalopoulos A, Stavridis G, Geroulanos S (1998) Severe Sepsis in Cardiac Surgical Patients. Eur J Surg 164:217-222
15. Rady MY, Ryan T, Starr NJ (1998) Perioperative determinants of morbidity and mortality in elderly patients undergoing cardiac surgery. Crit Care Med 26:225-235
16. Rauss A, Knaus WA, Patois E, LeGall JR, Loirat P, the French Multicentric group of ICU research (1990) Prognostic for recovery from multiple organ system failure: the accuracy of objective estimates of change for survival. Med Decis Making 10:155-162
17. Ryan TA, Rady MY, Bashour CA, Leventhal M, Lytle B, Starr NJ (1997) Predictors of outcome in cardiac surgical patients without prolonged intensive care stay. Chest 112:1035-1042
18. Turner JS, Morgan CJ, Thakrar B, Pepper JR (1995) Difficulties in predicting outcome in cardiac surgery patients. Crit Care Med 23:1843-1850
19. Weiss YG, Merin G, Koganov E, et al (2000) Postcardiopulmonary bypass hypoxemia: a prospective study on incidence, risk factors, and clinical significance. J Cardiothorac Vasc Anesth 14:506-513
Tabelle 1: Der additive CASUS
|
Organ System |
Variable |
Punkte |
||||
|
0 |
1 |
2 |
3 |
4 |
||
|
Respiratorisch |
PaO2/FiO2 (mmHg/%) |
Extubiert |
> 250 |
151-250 |
75-150 |
< 75 |
|
Renal |
S. Kreatinin (mg/dl) |
< 1.2 |
1.2-2.2 |
2.3-4.0 |
4.1-5.5 |
> 5.5 |
|
CVVH/Dialyse |
Nein |
-- |
-- |
-- |
Ja |
|
|
Hepatisch |
S. Bilirubin (mg/dl) |
< 1.2 |
1.2-3.5 |
3.6-7.0 |
7.1-14.0 |
> 14.0 |
|
Kardiovasculär |
PAR = HF x ZVD/MAD |
< 10.1 |
10.1-15.0 |
15.1-20.0 |
20.1-30.0 |
> 30.0 |
|
Laktat (mmol/l) |
< 2.1 |
2.1-4.0 |
4.1-8.0 |
8.1-12.0 |
> 12.0 |
|
|
IABP |
Nein |
-- |
-- |
-- |
Ja |
|
|
VAD |
Nein |
-- |
-- |
-- |
Ja |
|
|
Koagulation |
Thrombozyten x 10³/µL |
> 120 |
81 – 120 |
51 – 80 |
21 – 50 |
< 21 |
|
Zentrales Nervensystem |
Neurologischer Status |
Normal |
-- |
Verwirrt |
Sediert |
Diffuse Neuropathie |
CVVH: Kontinuierliche venovenöse Hämofiltration; FiO2: Fraktion eingeatmeter Sauerstoff; HF: Herzfrequenz; IABP: Intraaortale Ballonpumpe MAD: Mittlerer arterieller Druck; PaO2: Arterieller Sauerstoffpartialdruck; PAR: Druck adjustierte Herzfrequenz; S. Bilirubin: Serum Bilirubin; S. Kreatinin: Serum Kreatinin; VAD: Herzunterstützungssystem; ZVD: Zentral venöser Druck.
Tabelle 2: Zusammenfassung der Variablen des logistischen CASUS und den dazugehörigen β - Koeffizienten
|
Variable |
β – Koeffizient |
|
|
PaO2/FiO2 (mmHg/%) |
-0.0013498 |
|
|
S. Kreatinin (mg/dl) |
0.3063634 |
|
|
CVVH/ Dialyse |
Nein |
0 |
|
Ja |
0.4109223 |
|
|
S. Bilirubin (mg/dl) |
0.2214784 |
|
|
PAR = HF x ZVD/MAD |
0.0642751 |
|
|
Laktat (mmol/l) |
0.2115760 |
|
|
IABP |
Nein |
0 |
|
Ja |
0.6770239 |
|
|
VAD |
Nein |
0 |
|
Ja |
2.2976240 |
|
|
Thrombozyten x 10³/µL |
-0.0042251 |
|
|
Neuro-logischer
Status |
Normal |
0 |
|
Verwirrt |
0.4736275 |
|
|
Sediert |
0.7020852 |
|
|
Diffuse Neuropathie |
1.4715528 |
|
|
Intensivtag |
1 |
0 |
|
2 |
0.0097085 |
|
|
3 |
0.8372058 |
|
|
4 |
1.0426010 |
|
|
5 |
1.2561380 |
|
|
6 |
1.4975238 |
|
|
7 |
1.6260023 |
|
|
8 |
1.9023001 |
|
|
9 |
2.1064412 |
|
|
10 |
2.2268852 |
|
|
11 |
2.2597632 |
|
|
12 |
2.3782868 |
|
|
13 - ∞ |
2.5289064 |
|
|
Konstante |
-5.6412079 |
|
CVVH: Kontinuierliche venovenöse Hämofiltration; FiO2: Fraktion eingeatmeter Sauerstoff; HF: Herzfrequenz; IABP: Intraaortale Ballonpumpe MAD: Mittlerer arterieller Druck; PaO2: Arterieller Sauerstoffpartialdruck; PAR: Druck adjustierte Herzfrequenz; S. Bilirubin: Serum Bilirubin; S. Kreatinin: Serum Kreatinin; VAD: Herzunterstützungssystem; ZVD: Zentral venöser Druck.
Tabelle 3: Operative Eingriffe
|
Operation |
Anzahl |
% |
|
Isolierte Bypasschirurgie (Offpump-Technik) |
2144 |
52.9 |
|
(723) |
||
|
Isolierte Klappenchirurgie (minimal-invasive Chirurgie) |
923 |
22.8 |
|
(225) |
||
|
Kombinierte Bypass- & Klappenchirurgie |
538 |
13.3 |
|
Aortenchirurgie |
254 |
6.2 |
|
Herztransplantation |
42 |
1.0 |
|
Andere (angeborene Herzfehler, Herztumoren, pulmonare Embolektomie, Implantation von Herzunterstützungssystemen, u.a.) |
153 |
3.8 |
|
Total |
4054 |
100 |
Tabelle 4: Ergebnisse der OCC, der Diskriminierung (ROC-Analyse), der DeLong Methode und der Kalibrierung (O/E Verhältnis) für den additiven und logistischen CASUS von Tag 1 bis Tag 13
|
Intensiv- tag (n) |
CASUS |
OCC |
ROC-Analyse |
DeLong |
Kal. |
|
|
% |
AUC |
95%-KI |
p-Wert* |
O/E |
||
|
1 (4054) |
Add |
95.4 |
0.915 |
0.896 - 0.935 |
0.1631 |
0.6304 |
|
Log |
96.0 |
0.921 |
0.901 - 0.940 |
1.0006 |
||
|
2 (4008) |
Add |
96.6 |
0.966 |
0.956 - 0.975 |
0.8541 |
0.6264 |
|
Log |
96.8 |
0.963 |
0.952 - 0.974 |
0.9973 |
||
|
3 (1847) |
Add |
93.6 |
0.941 |
0.926 - 0.956 |
0.5311 |
0.7946 |
|
Log |
94.0 |
0.946 |
0.931 - 0.961 |
0.9984 |
||
|
4 (1257) |
Add |
91.6 |
0.931 |
0.913 - 0.949 |
0.2066 |
0.8320 |
|
Log |
92.8 |
0.939 |
0.921 - 0.957 |
0.9992 |
||
|
5 (902) |
Add |
89.8 |
0.918 |
0.896 - 0.941 |
0.0269 |
0.8735 |
|
Log |
90.9 |
0.932 |
0.911 - 0.953 |
0.9984 |
||
|
6 (696) |
Add |
88.4 |
0.903 |
0.876 - 0.931 |
0.0021 |
0.9394 |
|
Log |
90.5 |
0.919 |
0.894 - 0.945 |
1.0020 |
||
|
7 (557) |
Add |
87.1 |
0.903 |
0.875 - 0.930 |
0.0093 |
0.9593 |
|
Log |
88.2 |
0.916 |
0.889 - 0.942 |
0.9995 |
||
|
8 (461) |
Add |
85.9 |
0.903 |
0.873 - 0.933 |
0.0210 |
1.0190 |
|
Log |
88.1 |
0.914 |
0.885 - 0.944 |
1.0004 |
||
|
9 (387) |
Add |
85.3 |
0.881 |
0.842 - 0.920 |
0.0509 |
1.0904 |
|
Log |
86.3 |
0.890 |
0.854 - 0.926 |
0.9994 |
||
|
10 (343) |
Add |
84.5 |
0.867 |
0.822 - 0.912 |
0.1324 |
1.1050 |
|
Log |
84.8 |
0.874 |
0.832 - 0.916 |
1.0004 |
||
|
11 (317) |
Add |
84.5 |
0.868 |
0.822 - 0.915 |
<.0001 |
1.1076 |
|
Log |
85.9 |
0.889 |
0.847 - 0.931 |
1.0011 |
||
|
12 (289) |
Add |
83.7 |
0.865 |
0.815 - 0.915 |
<.0001 |
1.1564 |
|
Log |
85.5 |
0.885 |
0.843 - 0.928 |
1.0004 |
||
|
13 (269) |
Add |
86.2 |
0.877 |
0.828 - 0.925 |
<.0001 |
1.1934 |
|
Log |
86.2 |
0.901 |
0.861 - 0.941 |
1.0015 |
||
95%-KI: 95%-Konfidenz Intervall; Add: additiv; AUC: Area Under ROC-Kurve; CASUS: Cardiac Surgery Score; Kal.: Kalibrierung; Log: logistisch; O/E: observed/expected; OCC: Overall correct classification, Geamtprozentsatzes der „Richtigen“ in der Klassifizierungstabelle; ROC: Receiver Operating Characteristic.
*: zeigt den p-Wert nach der
DeLong Methode, die das additive und das logistische Modell vergleicht. Ein
p-Wert < 0.05 zeigt eine signifikant größere AUC des logistischen Modells
Tabelle 5: Klinische Werte der beiden Beispielpatienten
|
Organsystem |
Patient A |
Patient B |
|
Oxygenierungsindex (mmHg/%) |
160 |
Extubiert |
|
Kreatinin (mg/dl) |
0.5 |
1.58 |
|
CVVH/Dialyse |
Nein |
Ja |
|
Bilirubin (mg/dl) |
0.4 |
12.75 |
|
PAR (HF / ZVD / MAD) |
18.9 (90 / 13 / 62) |
29.4 (111 / 18 / 68) |
|
Laktat (mmol/l) |
11.1 |
1.5 |
|
IABP |
Nein |
Nein |
|
VAD |
Nein |
Nein |
|
Thrombozyten (x 10³/µL) |
97 |
Normal |
|
Neurologischer Status |
Sediert |
Normal |
|
Dauer des Intensivaufenthalts |
3 Stunden |
17 Tage |
|
Additiver CASUS |
11 Punkte |
11 Punkte |
|
Logistischer CASUS |
14.9 % |
75.9 % |
Grafik 1: Receiver Operating Characteristic Kurven des additiven und logistischen Modells an Tag 1 und Tag 2
Grafik 2: Kalibrierung nach Grunkemeier mit einem Vergleich des additiven und logistischen Modells von Tag 1 bis Tag 13
Grafik 3: Der Verlauf des β-Koeffizienten der Variable “Intensivtag” von Tag 1 bis Tag 25